Что такое фракталы и как они устроены?

Изучение фракталов на рубеже XIX и XX веков носило скорее эпизодический, нежели систематический характер, потому что раньше математики в основном изучали «хорошие» объекты, которые поддавались исследованию при помощи общих методов и теорий. В 1872 году немецкий математик Карл Вейерштрасс строит пример непрерывной функции, которая нигде не дифференцируема. Однако его построение было целиком абстрактно и трудно для восприятия. Поэтому в 1904 году швед Хельге фон Кох придумал непрерывную кривую, которая нигде не имеет касательной, причем ее довольно просто нарисовать. Оказалось, что она обладает свойствами фрактала. Один из вариантов этой кривой носит название «снежинка Коха».

Идеи самоподобия фигур подхватил француз Поль Пьер Леви, будущий наставник Бенуа Мандельброта. В 1938 году вышла его статья «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому», в которой описан еще один фрактал — С-кривая Леви. Все эти вышеперечисленные фракталы можно условно отнести к одному классу конструктивных (геометрических) фракталов.

Другой класс — динамические (алгебраические) фракталы, к которым относится и множество Мандельброта. Первые исследования в этом направлении начались в начале XX века и связаны с именами французских математиков Гастона Жулиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный мемуар Жулиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жулиа — целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно. Несмотря на то что это работа прославила Жулиа среди математиков того времени, о ней довольно быстро забыли. Вновь внимание к ней обратилось лишь полвека спустя с появлением компьютеров: именно они сделали видимыми богатство и красоту мира фракталов.

В 1982 году вышла книга Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил ее. Основной упор в своем изложении Мандельброт сделал не на тяжеловесные формулы и математические конструкции, а на геометрическую интуицию читателей. Благодаря иллюстрациям, полученным при помощи компьютера, и историческим байкам, которыми автор умело разбавил научную составляющую монографии, книга стала бестселлером, а фракталы стали известны широкой публике. Их успех среди нематематиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения. Когда персональные компьютеры стали достаточно мощными, появилось даже целое направление в искусстве — фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера. Сейчас в интернете можно легко найти множество сайтов, посвященных этой теме.

Как уже отмечалось выше, один из природных объектов, имеющих фрактальные свойства, — это береговая линия. С ним, а точнее, с попыткой измерить его длину, связана одна интересная история, которая легла в основу научной статьи Мандельброта, а также описана в его книге «Фрактальная геометрия природы».

Речь идет об эксперименте, который поставил Льюис Ричардсон — весьма талантливый и эксцентричный математик, физик и метеоролог. Одним из направлений его исследований была попытка найти математическое описание причин и вероятности возникновения вооруженного конфликта между двумя странами. В числе параметров, которые он учитывал, была протяженность общей границы двух враждующих стран. Когда он собирал данные для численных экспериментов, то обнаружил, что в разных источниках данные об общей границе Испании и Португалии сильно отличаются. Это натолкнуло его на следующее открытие: длина границ страны зависит от линейки, которой мы их измеряем. Чем меньше масштаб, тем длиннее получается граница. Это происходит из-за того, что при большем увеличении становится возможным учитывать все новые и новые изгибы берега, которые раньше игнорировались из-за грубости измерений. И если при каждом увеличении масштаба будут открываться ранее не учтенные изгибы линий, то получится, что длина границ бесконечна! Правда, на самом деле этого не происходит — у точности наших измерений есть конечный предел. Этот парадокс называется эффектом Ричардсона.

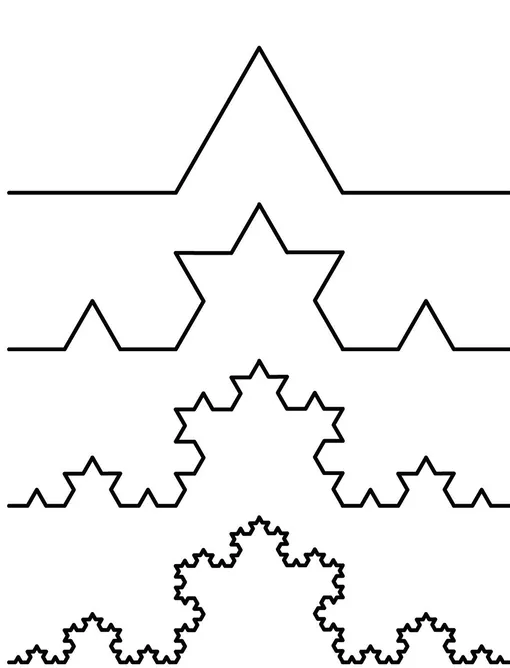
Алгоритм построения конструктивного фрактала в общем случае таков. Прежде всего нам нужны две подходящие геометрические фигуры, назовем их основой и фрагментом. На первом этапе изображается основа будущего фрактала. Затем некоторые ее части заменяются фрагментом, взятым в подходящем масштабе, — это первая итерация построения. Затем у полученной фигуры снова некоторые части меняются на фигуры, подобные фрагменту, и т. д. Если продолжить этот процесс до бесконечности, то в пределе получится фрактал.

Рассмотрим этот процесс на примере кривой Коха. За основу кривой Коха можно взять любую кривую (для «снежинки Коха» это треугольник). Но мы ограничимся простейшим случаем — отрезком. Фрагмент — ломаная, изображенная сверху на рисунке. После первой итерации алгоритма в данном случае исходный отрезок совпадет с фрагментом, затем каждый из составляющих его отрезков сам заменится на ломаную, подобную фрагменту, и т. д. На рисунке показаны первые четыре шага этого процесса.

Фракталы этого типа возникают при исследовании нелинейных динамических систем (отсюда и название). Поведение такой системы можно описать комплексной нелинейной функцией (многочленом) f (z). Возьмем какую-нибудь начальную точку z0 на комплексной плоскости (см. врезку). Теперь рассмотрим такую бесконечную последовательность чисел на комплексной плоскости, каждое следующее из которых получается из предыдущего: z0, z1=f (z0), z2=f (z1), ... zn+1=f (zn). В зависимости от начальной точки z0 такая последовательность может вести себя по-разному: стремиться к бесконечности при n -> ∞; сходиться к какой-то конечной точке; циклически принимать ряд фиксированных значений; возможны и более сложные варианты.

Таким образом, любая точка z комплексной плоскости имеет свой характер поведения при итерациях функции f (z), а вся плоскость делится на части. При этом точки, лежащие на границах этих частей, обладают таким свойством: при сколь угодно малом смещении характер их поведения резко меняется (такие точки называют точками бифуркации). Так вот, оказывается, что множества точек, имеющих один конкретный тип поведения, а также множества бифуркационных точек часто имеют фрактальные свойства. Это и есть множества Жулиа для функции f (z).

Множество Мандельброта строится несколько иначе. Рассмотрим функцию fc (z) = z^2+с, где c — комплексное число. Построим последовательность этой функции с z0=0, в зависимости от параметра с она может расходиться к бесконечности или оставаться ограниченной. При этом все значения с, при которых эта последовательность ограничена, как раз и образуют множество Мандельброта. Оно было детально изучено самим Мандельбротом и другими математиками, которые открыли немало интересных свойств этого множества.

Видно, что определения множеств Жулиа и Мандельброта похожи друг на друга. На самом деле эти два множества тесно связаны. А именно, множество Мандельброта — это все значения комплексного параметра c, при которых множество Жулиа fc (z) связно (множество называется связным, если его нельзя разбить на две непересекающиеся части, с некоторыми дополнительными условиями).

Фракталы и жизнь

В наши дни теория фракталов находит широкое применение в различных областях человеческой деятельности. Помимо чисто научного объекта для исследований и уже упоминавшейся фрактальной живописи, фракталы используются в теории информации для сжатия графических данных (здесь в основном применяется свойство самоподобия фракталов — ведь чтобы запомнить небольшой фрагмент рисунка и преобразования, с помощью которых можно получить остальные части, требуется гораздо меньше памяти, чем для хранения всего файла). Добавляя в формулы, задающие фрактал, случайные возмущения, можно получить стохастические фракталы, которые весьма правдоподобно передают некоторые реальные объекты — элементы рельефа, поверхность водоемов, некоторые растения, что с успехом применяется в физике, географии и компьютерной графике для достижения большего сходства моделируемых предметов с настоящими. В радиоэлектронике выпускают антенны, имеющие фрактальную форму. Занимая мало места, они обеспечивают вполне качественный прием сигнала. Экономисты используют фракталы для описания кривых колебания курсов валют (это свойство было открыто Мандельбротом). На этом мы завершим эту небольшую экскурсию в удивительный по красоте и разнообразию мир фракталов.