Эта банальная логическая задача стара как мир. Все очень просто: посчитайте каждый отдельный треугольник, затем сложите все различные комбинации маленьких треугольников и обязательно не забудьте про большую общую фигуру. Вы ведь так делаете? При всей своей простоте, эта задача всегда вызывает массу споров и сотни комментариев с ответами в диапазоне от четырех до 45 (боже, откуда столько?).
Непростая задача для первых классов: а вы сможете решить?
Мы все чертовски любопытны по своей природе, и нет ничего проще, чем поставить наши умы в тупик. Достаточно всего-то на первый взгляд простейшей задачки, и вот рабочие процессы тут же отодвинуты на второй план, никто не отвечает на телефонные звонки, дети кричат, но взрослые ни на что не реагируют. Сколько вы видите треугольников на изображении? Только не спешите, подумайте как следует. А теперь еще подумайте...
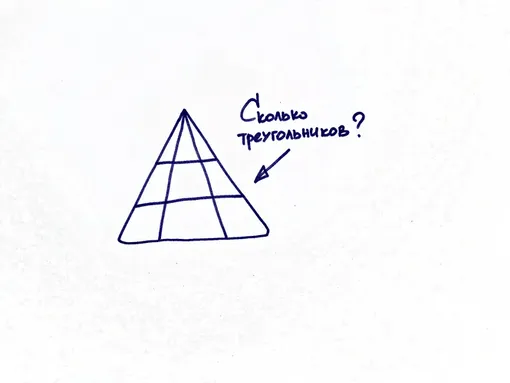
Давайте сначала вспомним из школьной программы, что же такое треугольник. В евклидовом пространстве это геометрическая фигура (он же многоугольник с фиксированным числом углов), образованная тремя отрезками (стороны треугольника), которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Возможно, мы повторно взорвем ваш мозг, но есть так называемый вырожденный треугольник, вершины которого таки лежат на одной прямой. Живите теперь с этим.
Продолжение ниже
Видео
Продолжение
Отрезок, соединяющий вершину с точкой на противоположной стороне, называется чевианой. Обычно под чевианой понимают не один такой отрезок, а один из трех отрезков, проведенных из трех разных вершин треугольника и пересекающихся в одной точке. В нашем случае есть две чевианы, которые спускаются из верхнего угла на нижнюю сторону большой фигуры. Благодаря треугольнику появилась тригонометрия, планиметрия, а еще используя эту простую фигуру, люди научились составлять карты, измерять участки и конструировать. Даже «Черный квадрат» Малевича должен был называться «Черный китайский треугольник», и не спрашивайте, почему. Казимир Северинович унес эту тайну с собой на тот свет. В общем, при всей своей простоте полезная штука. Но мы отвлеклись.
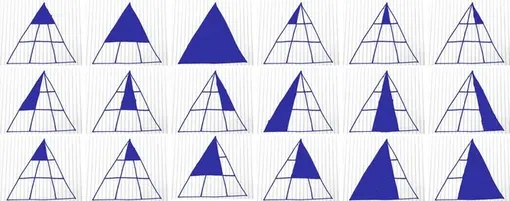
Итак, еще раз посмотрим на нашу задачу. Те из вас, кто везде торопится, выдают сразу варианты ответов: шесть треугольников, 16, 22. Многие насчитывают 18 искомых фигур. Кто подотошнее считает, что на изображении нет ни одной прямой линии, а некоторые углы — не углы вовсе. Ну, конечно, это же нарисовано от руки! Для таких тут вообще нет ни одного треугольника. Зануды. Если вы все еще не нашли ответ и пытаетесь прочитать его в этом тексте, то остановитесь и просто посчитайте чертовы треугольники.
Ладно, давайте не будем играть в «Поле Чудес», а посмотрим на задачу с точки зрения науки. Единственный способ образовать треугольники на рисунке — это если верхний угол является частью каждого треугольника. Основание треугольника должно быть одним из трех горизонтальных уровней ниже. Получается, три уровня, на каждом вы можете выбрать базу для шести разных способов построения фигуры. В сумме выходит восемнадцать или три раза по шесть треугольников. Все варианты научного решения так или иначе крутятся вокруг этого способа. И да, вы же не забыли посчитать треугольник у стрелочки? Ладно, это была шутка. Или все же посчитали?
Загружаем